Graphing Motion Using Motion Detectors

Title of lesson: GRAPHING MOTION USING MOTION DETECTORS

Author: Theresa Hogan

(largely based from Jonas Trevino’s “Graphing with Motion Detectors” lesson plan for his group’s project: “How Can You Represent Motion?”- PBI Fall ‘04)

Length of lesson: 2 – 3 days

Grade level: Algebra I / Algebra II

Source of the lesson:

http://uteach.utexas.edu/~gdickinson/pbi/PBIFall04/Motion/Content/motion.htm

Other sources:

http://education.ti.com/educationportal/activityexchange/activity_detail.do?cid=us&activityid=5559 (for in-class activity)

TEKS addressed:

A.1 (d) represent relationships among quantities using concrete models, tables, graphs, diagrams, verbal descriptions, equations, and inequalities

A.6 (a) develop the concept of slope as rate of change and determine slopes from graphs, tables, and algebraic representations

2A.1 (b) collect and organize data, make and interpret scatterplots, fit the graph of a function to the data, interpret the results, and proceed to model, predict, and make decisions and critical judgments

I.      Overview

Students can use motion detectors to create distance vs. time graphs. They can also develop a basic understanding of the relationship between the x and y variables (distance vs. time) by participating in such activities such as practice problems involving the graphs created.

II.  Performance or learner outcomes

            Students will be able to:

§       Assemble and disassemble the calculator, CBLs, and motion detectors

§       Analyze the graph coordinate system

§       Explain and apply the distance versus time relationship

III. Resources, materials and supplies needed

§       Calculators

§       CBLs

§       Motion Detectors

§       Connector Cables

IV. Supplementary materials, handouts

§       Assembly diagram (can find on TI website)

§       Graphing worksheet activity (83tg_expl_Act02.pdf on TI website, make changes/additions as desired to questions the worksheet asks)

§       Quiz worksheet

Five-E Organization

Teacher Does                    Probing Questions                    Student Does      

Engage: Given a graph, ask them to make up any hypothetical scenario that the graph could represent. Ask students to identify what the x and y variables on the graph represent. The goal of this engagement is to let students know the complete freedom of what graphs can be used to represent, whether it is real life or not. Teacher will encourage students to find unique relationships in their graphs and representations.

For your scenario, what do the x and y variables represent? Why did you draw your graph like you did?

Student should create scenarios with given graphs and explain to class how they came up with the scenario. They will also explain what the x and y variables on the graph represent.

Explore: Divide the class into appropriate size groups for the number of motion detectors available. Give written instructions and explain how to set up the calculator – CBR – motion detectors, and allow time for set-up. Explain how the motion detectors work. Instruct the students to experiment with the motion detectors and allow time for experimentation.

We will ask a number of students for any observations about the connection between motion and the resultant graph.

Students set up the calculator – CBR – motion detectors. The students should experiment with the motion detectors.

Explain: Ask students for hypotheses about what the x-axis and y-axis represent for the graphs created by the motion detectors. Move on when teacher is satisfied that students grasp the distance vs. time relationship (x = time, y = distance).

Ask some or all questions (as needed) from the following list: 1. What physical property is represented along the x-axis? 2. What are the units? 3. What physical property is represented along the y-axis? 4. What are the units? 5. How far from the CBR do you think you should stand to begin? 6. Should you walk towards or away from the wall for a segment that slopes up? 7. Why? 8. Should you walk towards or away from the wall for a segment that slopes down? 9. Why? 10. What should be done for a flat segment? 11. For the given graph, did you move towards or away from the graph? 11. How far did you travel? (Questions suggested by Kate Brien)

Students should answer questions appropriately. The students’ responses to the questions should indicate whether or not they have an understanding of the concepts.

Extend / Elaborate: Teacher will ask students for ideas on what process(es) they would use to create certain segments on given graphs. Teacher will draw a graph or two (as time allows) on the board and ask the students to recreate the graph with their motion detectors. (Allow time to attempt the graphing.)

How would you need to move to create an upward sloping section of the graph like this? What about this section that looks like half of a bowl?

Students explain how they would create certain segments on the graph. Students recreate graphs using the motion detector and give a brief explanation on how they created each graph.

Evaluate: To see what the students’ understanding of the connection between their actions with the motion detectors and the time versus distance graphs they create, an evaluative quiz/worksheet (“QUIZ”) will be administered. It will ask summative questions such as what the x-axis and y-axis represent, and it will have graphs for which they must explain how a motion detector could be used to recreate them.

The quiz will hopefully be a positive indicator of their understanding of the motion detectors and graphs.

QUIZ

1. Could you walk to produce a horizontal line?

Give reasons for your answer.

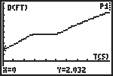
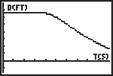
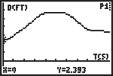
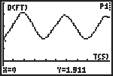
2. For each of the graphs below, describe the motion of the walker.

A B C D

A:

B:

C:

D: