LESSON PLAN
Name: Danielle Ortega
Title of lesson: Introduction to Parabolas
Date of lesson: Unit: Motion in Baseball, Monday of Week 3
Length of lesson: 50 minutes
Description of the class:
Name
of course:
Algebra II
Grade
level: 11th
Grade
Honors
or regular: Either
Source of the lesson:
Construction
of Parabola Activity:
http://utopia.utexas.edu/lesson_plans/2005/gallo_algebra_2_parabola.php
TEKS addressed:
§111.32. Algebra I (One Credit).
(d) Quadratic and other nonlinear
functions: knowledge and skills and performance descriptions.
(1) The student understands that the
graphs of quadratic functions are affected by the parameters of the function and
can interpret and describe the effects of changes in the parameters of
quadratic functions.
I.
I. Overview
Students will learn basic
characteristics of parabolas and that quadratic functions have parabolas as
their graphs.
II. Performance or learner outcomes
Students
will be able to:
· Identify and
recognize parabolas as the graphs of quadratic functions.
· Define a parabola as the set of points which are all
equidistant from the focus and directrix.
· Determine the
focus, directrix, vertex, and axis of symmetry of a
parabola from its graph.
III. Resources, materials and supplies needed
Overheads: Satellite dish, cross-section of satellite
dish, graphs of various
quadratic functions.
IV. Supplementary materials, handouts.
Handout/Worksheet: Construction of a Parabola
Five-E Organization
Teacher
Does Probing Questions Student
Does
|
Engage: Teacher will show a
picture of a satellite dish and a picture of a cross section of a satellite
dish. In
a while, we’ll learn a little bit about how algebra makes satellite dishes
work. |
Does anyone know the
mathematical name for this shape (referring to cross section)? Where else do you see this
shape? |
Parabola (some may already
know, most probably not) Various answers. |
|
Explore: Students will follow the
instructions on the handout to construct two different parabolas and will
record their observations. Teacher
will circulate room, asking questions and making sure the students are
correctly constructing the parabolas. |
What do you notice
about the shape of the graphs you’ve made? What happened when you
placed the horizontal line closer to the center point? What do all of the points
for each graph have in common? What happened when you
picked a horizontal line above the center point? |
Curves, U-shaped. Shape got steeper,
skinnier. All the same distance from
the center point and the line. (Teacher may have to lead them to this
conclusion). The curve opened downward,
upside down U. |
|
Explain: Two
students will use the overhead to draw one of their parabolas. One student should draw an upward facing
parabola and the other should draw a downward facing parabola. Teacher will then put up
an overhead of the graph of the function y = x2 . We will use this picture to introduce important vocabulary such as parabola, focus,
directrix, axis of symmetry, and vertex, relating
these to the points and lines the encountered in the exploration activity. Teacher will then place several
picture of parabolas on the overhead with their respective functions (y =…). At first, students will verbally identify
the parts of the parabolas. For the last few, students
will individually identify the parts of the parabolas and record them on a
piece of paper along with the functions.
The teacher will collect these as an evaluation. Teacher will reconvene the
class to emphasize that quadratic functions always have parabolas as their
graphs. |
Ask
same questions as above to entire class. Does
this graph look like the ones you just drew? What
is the focus? Directrix? Axis of symmetry? Vertex? What
do you notice about the functions for all of these parabolas? |
Yes, same shape. Students will give focus, directrix, vertex and and axis
of symmetry for each parabola.. They all have an x2
in them. All are degree 2. |
|
Extend / Elaborate: Teacher will put the
pictures of the satellite dish back up on the overhead. The teacher will explain
that the parabolic shape of the dish reflects all the incoming signals to the
receiver and that’s how satellite dishes work. |
(Showing cross section)
What shape is the cross-section of the satellite dish? What part of the
parabola is the receiver of the satellite dish? (Showing whole satellite
dish) Is the satellite dish made up of just one parabola? Do they all have the same
focus? |
The cross section is a
parabola. The focus. No, there are lots of
parabolas (lots of cross-sections). Yes, all have the receiver
as their focus. |
|
Evaluate: Teacher will check for understanding at various
points of the lesson and collect papers from Explanation section. Teacher
will ask a few wrap-up questions. |
Name
the parts of the parabola we learned today and how they affect the parabola. What
kinds of functions have parabolas as their graphs? |
Students will describe the
vertex, focus, directrix, and axis of symmetry. Quadratic functions. |
Worksheet below:
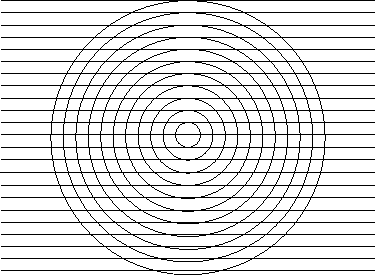
Construction of a Parabola
![]()

![]()
- Number all of the horizontal lines above from 1 to 25, starting with the bottom line as #1. Draw a vertical line down the center of the grid.
- Assume the width between each line is 1 unit. Notice that the radius of the innermost circle is 1 unit and the radius for each successive circle increases by 1.
- Label the center point of the circles as F. Note that F should lie on the vertical line you drew in step 1.
- Choose any horizontal line below line number 13 and darken in with your pencil. Hint: choosing an odd-numbered line makes the construction a little simpler.
- Find the midpoint between point F and the horizontal line you chose and label it V. This point should lie on the vertical line from step 1.
- Identify the next largest circle from the one on which V lies and the line numbered 1 GREATER than the line on which V lies. Draw in the two intersection points of this circle and line.
- Continue performing step 6, moving progressively further and further outward through the grid, until you reach the largest circle, making sure to draw in all the intersection points.
- Connect all the points you have just drawn.
- Now choose a horizontal line above line number 13 and darken it with your pencil. Again, choosing an odd-numbered line will make things simpler.
- Perform step 5 to label a new point V2.
- Perform step 6, except this time, draw in the 2 intersections of the next largest circle with the line numbered 1 LESS than the horizontal line on which your new V2 lies.
- Repeat as before until you reach the largest circle. Connect all the points you have just drawn.