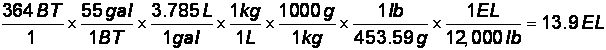Dimensional
Analysis
Name: Wade Green
Title of lesson: Dimensional Analysis
Date of lesson: TBD
Length of lesson: 1 hour
Description of the class:
Name
of course: Chemistry
Grade
level: 11
Honors
or regular: regular
Source of the lesson:
Original
idea from Robert Krulwich, ABC News
TEKS addressed:
112.45 (c) Knowledge and skills:
(2) Scientific processes. The
student uses scientific methods during field and laboratory investigations. The
student is expected to:
(C) express and
manipulate chemical quantities using scientific conventions and mathematical
procedures such as dimensional analysis, scientific notation, and significant
figures.
I.
Overview
Dimensional Analysis is just a fancy way of saying unit
conversion. Scientists regularly have
the need to convert a piece of data given in one unit system to another. Using a simple technique of multiplying
fractions and canceling units converts units between measurement systems and
applies the necessary prefixes for metric measurement units.
II. Performance or learner outcomes
Students
will be able to:
1.
Convert
between units of different measurement systems.
2.
Properly
apply unit prefixes to measurement figures.
3.
Convert
between types of measurements (i.e. volume to mass)
III. Resources, materials and supplies
needed
IV. Supplementary materials, handouts.
1. Conversion Factors Handout (1 per
student)
2.
Dimensional
Analysis Worksheet
Five-E
Organization
Teacher
Does Probing Questions
Student Does
|
Engage: How much does a hurricane
weigh?
To begin with, you would need to know
how much water is in a certain volume of air within a cloud. For that, you
could find the mass of a cubic meter of cloud air and then subtract the mass
of the non-water parts. Then all you need is the volume of the hurricane and
you’re set. This might sound complicated, but the
math is fairly easy and Chemists do the same type of calculations all the
time. Somewhere in every Chemistry textbook is a
list of constants and conversion factors for all sorts of units. Some of these are familiar and some are
not, but all of them are given with units. Some constants are even given more
than once with different units. If we have the units, it is easy to convert
one measurement to another with Dimensional Analysis.
|
If you wanted to know how much a
hurricane weighs, how would you go about it?
|
Likely
ideas: Measure
the density of the air and multiply by the volume of a hurricane. |
|
Explore: Dimensional analysis might sound like
a big scary topic, but it is just a fancy way of saying, “convert units” like
from centimeters to meters. Not all of
these will be easy enough to do in your head, so there is a technique for
converting whatever you have to whatever you need. All that’s
needed is multiplying fractions, canceling units, and a little imagination. To prove that this works for any units
where you have a conversion factor, we’re going to use some unique units in
our calculations. On the Conversion Factors Handout, you
will see some of the common conversions between customary and metric
measurements as well as a few non-customary units. For any dimensional conversion, you
will multiply a series of fractions together to convert to the units you
want. You should always start off by
writing the information you have on the left using the given units. On the
right side, write the units you want to end up with. Between these two, find a series of
conversions that change what you have to what you want. Example: What is the mass of two elephants in
kilograms?
Example 2: What is the mass of 10 bathtubs of
water in elephants? See below… |
Who can tell me what 500 cm is in
meters? Can you multiply 3/2 x 1/3? |
Students should
be able to convert this to 5 m. Students
should be able to easily find the answer is 3/6 or ½. |
![]()
|
Explain: In class worksheet
Dimensional Analysis Worksheet |
|
|
|
Extend /
Elaborate: At the beginning of class, I asked how much a hurricane weighs. A newsman asked a meteorology professor
this question and she calculated that the average cloud contains an amount of
water equal to 100 elephants. If you apply this to a large storm cloud, you
get about 13,750 elephants. For a large hurricane, the number becomes 40
million elephants worth of water. How is that possible? You have to realize the enormous size of a
hurricane. If a hurricane has a radius of 675 miles and reaches a height of 35,000
ft., this works out to a volume of 1.39x1015 ft3. Using the professor’s calculation of 55
billion gallons of water in a hurricane, this converts to 0.15 mL of water per cubic foot.
|
|
|
|
Evaluate: Quiz |
|
|
Original idea
source:
Elephants in the Sky
Using the Largest Living Land Mammal to Calculate Cloud Mass
By Robert Krulwich
Sept. 3— Ever wonder how
much a cloud weighs? What about a hurricane? A meteorologist has done some
estimates and the results might surprise you.
Let's start with a very simple white puffy cloud — a
cumulus cloud. How much does the water in a cumulus cloud weigh? Peggy LeMone, senior scientist at the
"The water in the little cloud weighs about 550 tons," she
calculates. "Or if you want to convert it to something that might be a
little more meaningful … think of
elephants."
Floating Masses
Assume an elephant weighs about six tons, she says, that would mean that water
inside a typical cumulous cloud would weigh about one hundred elephants.
The thought of a hundred elephants-worth of water suspended in the sky begs
another question — what keeps it up there?
"First of all, the water isn't in elephant sized particles, it's in tiny tiny tiny particles,"
explains LeMone.
And those particles float on the warmer air that's rising below. But still, the
concept of so much water floating in the sky was surprising even to a
meteorologist like LeMone.
"I had no idea how much a cloud would weigh, actually, when I started the
calculations," she says.
Outweighing Elephant Populations
So how many elephant units of water are inside a big storm cloud … 10 times bigger all the way around than the "puffy" cumulus
cloud? Again, LeMone did the numbers: About 200,000
elephants.
Now, ratchet up the calculations for a hurricane about the size of
"What we're doing is weighing the water in one cubic meter theoretically
pulled from a cloud and then multiplying by the number of meters in a whole
hurricane," she explains.
The result? Forty million elephants.
That means the water in one hurricane weighs more than all the elephants on the
planet. Perhaps even more than all the elephants that have
ever lived on the planet.
And that is a lot of water.
|
Type of Cloud |
Gallons |
Tons of water |
Elephants |
Typical home pool |
|
Light cloud |
137,500 |
550 |
100 |
6.75 |
|
Puffy cumulus cloud |
275,000,000 |
1,100,000 |
200,000 |
13,750 |
|
Hurricane |
55,000,000,000 |
220,000,000 |
40,000,000 |
2,750,000 |
|
In other words a normal hurricane will have enough water to fill
46% of |
||||
Conversion
Factors
|
Symbol |
Unit |
= |
Unit |
Symbol |
|
lb. |
1 pound |
= |
453.59 grams |
g |
|
oz. |
1 ounce |
= |
28.35 grams |
g |
|
gal. |
1 gallon |
= |
4 quarts |
qt. |
|
gal. |
1 gallon |
= |
3.785 liters |
L |
|
BT |
1 bathtub |
= |
55 gallons |
Gal. |
|
ft. |
1 foot |
= |
30.48
centimeters |
cm |
|
EL |
1 elephant |
= |
12,000 pounds |
lb. |
|
BB |
1 basketball court length |
= |
94 feet |
ft. |
|
mi. |
1 mile |
= |
5280 feet |
ft. |
Metric system
prefixes
|
Prefix |
Multiplication
factor |
Symbol |
|
femto |
x 10-15 |
f |
|
pico |
x 10-12 |
p |
|
nano |
x 10-9 |
n |
|
micro |
x 10-6 |
μ |
|
milli |
x 10-3 |
m |
|
centi |
x 10-2 |
c |
|
kilo |
x 103 |
k |
|
mega |
x 106 |
M |
|
giga |
x 109 |
G |
Useful Extras:
1 L of water
weighs 1 kg.
1 m3
of water contains 10 L
Name__________________________
Date___________________________
Dimensional
Analysis Worksheet
Do the
following conversion problems. Be sure
to show your work.
- Mr. Green’s dog weighs about 43
kg. What is the dog’s weight in
elephants (EL)?
- A car is traveling at 55 miles per
hour, how many basketball courts (BB) does it cross per second?
- The average home pool holds 20,000
gallons of water. How many bathtubs
(BT) is this?
- How much does this water weigh in
elephants (EL)?
Dimensional Analysis
Worksheet Answer Key
Do the
following conversion problems. Be sure
to show your work.
- Mr. Green’s dog weighs about 43
kg. What is the dog’s weight in millielephants (mEL)?
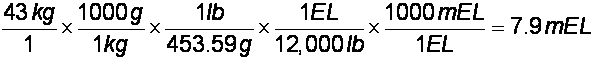
- A car is traveling at 55 miles per
hour, how many basketball courts (BB) does it cross per second?
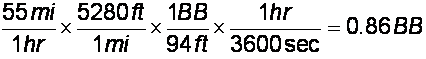
- The average home pool holds 20,000
gallons of water. How many bathtubs
(BT) is this?
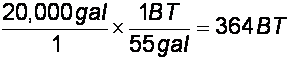
- How much does this water weigh in
elephants (EL)?